Lab #7
Transients in Second Order Reactive Systems

Purpose
To become familiar with the transient behavior of a simple RLC circuit.

The behavior of systems as an external energy source changes from one state to another is important not only in electric circuits, but also in other systems. The time taken to reach steady state under the new conditions, the changes (sometimes oscillatory) that the variables in the system go through in this process, the peak excursions of variable and the stability of the system are of concern. The period when the circuit goes from one steady state to another is the transient period of the system and understanding this phenomenon is the object of this experiment. 

Pre-Lab
For the series RLC circuit labeled Circuit 1 the characteristic equation is

With a Damping Coefficient (in rad/s) and Resonant Frequency of:

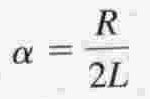
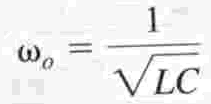
The circuit is considered Critically Damped when:

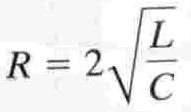
and Overdamped  and Underdamped if respectively:

1. Calculate R_Critical for a critically damped system.
2. Calculate 4R_Critical for a overdamped system..
3. Calculate (1/4)R_Critical for an underdamped system.
4. Use PSpice to simulate the voltage that will be monitored by Channel 2 of the oscilloscope (voltage across the capacitor). As we saw in Lab 6, in PSpice you can simulate a repetitive step response with using a VPULSE with the attributes on Circuit 2. Figure 1 describes what the attributes of the VPULSE are. To get the three responses on one PSpice simulation, copy Circuit 2 three times (changing the L1, R1 & C1 labels and the value of the resistors). Print the responses of V_RC (for the three values of R calculated above). Note: V_RC is the voltage at the Net Alias RC in Circuit 2. To add a Net Alias press the icon (located on the right had side) and follow the menus. Use the File/Print... menu option in PSpice to print the response instead of <PrntScr> key which uses way too much black ink. If you copied the circuit 3 times the Net Aliases must also be unique.
5. Calculate the resonant frequency of the circuit. (Remember the equation above gives the frequency as a radian frequency (rad/sec). You want a frequency in cycles/sec (Hz) and there are 2π radians in a cycle.)
6. Print out LabGradicules.pdf and bring it to the lab for sketching waveforms .
   

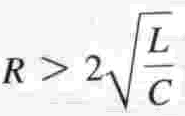
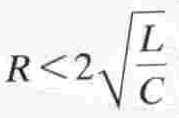
Equipment
Proto Board
Short pieces of wire
Resistors (three determined in the prelab)
Capacitor (one - 0.01µF)
Inductor (one - 25mH)
Multimeter
Function Generator
Oscilloscope

Procedure

Transients in RLC Circuits
1. Construct the RLC circuit as shown in Circuit 1. Apply a 2Vpp (2V peak to peak) 1kHz square wave. Use the closest standard value resistor for R_Critical that you calculated in Section 1 of the PreLab.
Note: Remember, a square wave can be considered as a repetitive step voltage that will enable you to obtain a steady display on the oscilloscope..

2. Using the oscilloscope, observe the applied voltage on Channel 1 and the voltage across the capacitor C on Channel 2. Carefully sketch the superimposed waveforms showing the horizontal and vertical scales (voltage and time per division) and the number of divisions.

3. Measure the Rise Time of the step response. Indicate the rise time of the voltage on the sketch for Section 2 above. Show me how.

4. Change R to the closest standard value for 4R_Critical that you calculated in Section 2 of the Pre-Lab. Change the Function Generator to 400 Hz and carefully sketch the superimposed waveforms. Measure the rise time and indicate it on the sketch. Show me how

5. Change R to the closest standard value for (1/4)R_Critical that you calculated in Section 3 of the Pre-Lab. Change the Function Generator back to 1 kHz and carefully sketch the superimposed waveforms. Measure the rise time and indicate it on the sketch. Show me how

6. Replace R with a short circuit. Record the period of the first cycle of the ringing that occurs. To make the most accurate measurement:

• Change the trigger to trigger on the positive slope.
• Increase the speed of the time base to display the first two cycles of the ringing on the oscilloscope screen.
• Measure the number of divisions from the top of the first cycle to the top of the second cycle. The period is then: (# of divisions) * (SEC/DIV)

7. Calculate the frequency of the ringing. The frequency in hertz or cycles/second is 1/period in seconds/cycle.

Analysis
1. Carefully sketch the observed waveforms and indicate the horizontal and vertical scales for parts 2, 4 and 5.

2. Compare the responses obtained with what was expected. Discuss what each response represents.

3. Compare the frequency of the ringing (Section 7 of the Procedure) with the resonant frequency calculated in Section 5 of the Pre-Lab. Why was R set to 0Ω for this measurement?

4. Measure the Rise Times of the simulated PSpice responses (done in Section 4 of the Pre-Lab) and compare them to those measured in Sections 3, 4 and 5 of the Procedure.

5. Compare and comment on the rise times noted in parts 3, 4 and 5 of the Procedure.